动态规划

动态规划的思想是把一个大问题拆分成一个个小问题，并在解决这些小问题之后把其最优解保留下来，解后面的大问题时会用到这些小问题的解

例一：01背包：现有音响（3000元，重4），电脑（2000元，重3），吉他（1500元，重1），你有一个能装最大重量为4的背包，现在请找出能够获取最大利益的装货方式

一开始我们只考虑吉他，这种情况下，背包容量从1-4的最优装法都只有装入吉他这一种，最终的解为(1500)

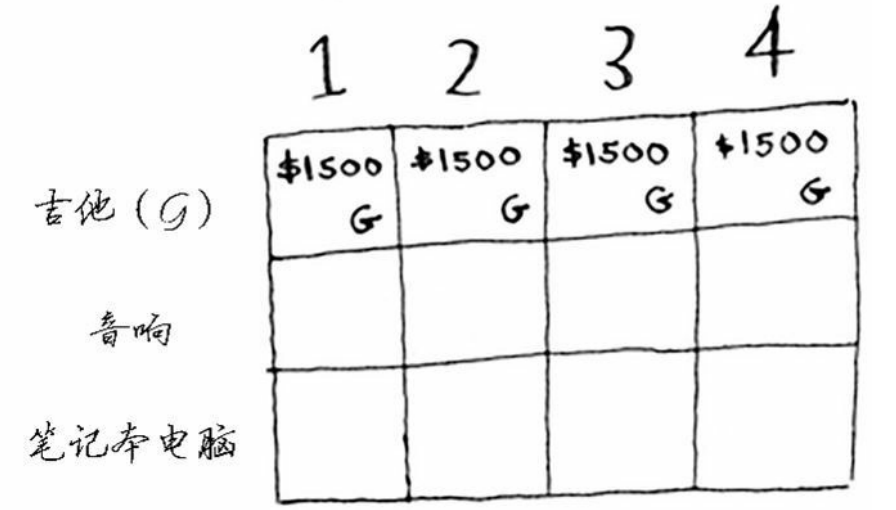
接下来我们把音响也加入考虑，当背包容量在1-3的时候，依旧是只有拿吉他这种解法，但当容量到4的时候，这时候选择往背包里面装入音响比装入吉他利益要来的更高，所以我们在4这一格选择就放入音响，得到了这一行的结果

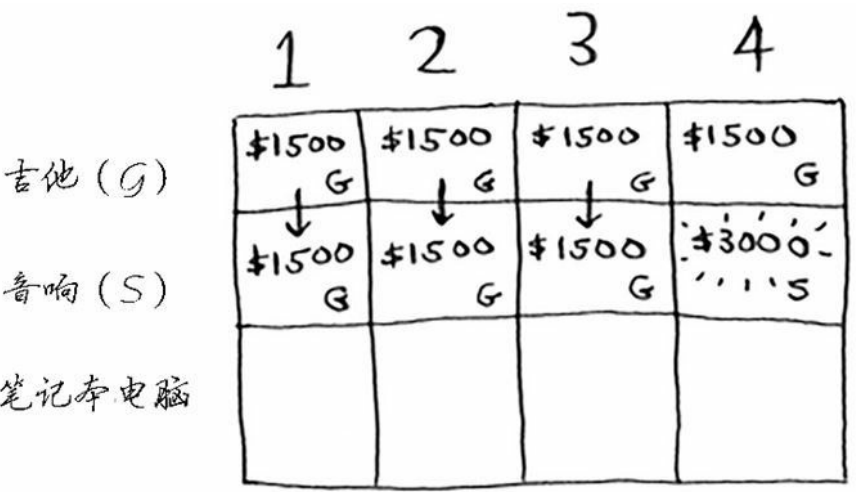
接下来我们把电脑加入考虑，当背包容量是1-2的时候，依旧还是拿吉他（1500），但当变成3的时候，我们发现选择拿电脑更合适（2000），而到4的时候，我们发现，如果拿电脑，我们还余下1的余量，而余量1的最优解是1500，于是我们同时拿了电脑和吉他，共3500，大于只拿音响的3000，于是最终解变成了电脑与吉他

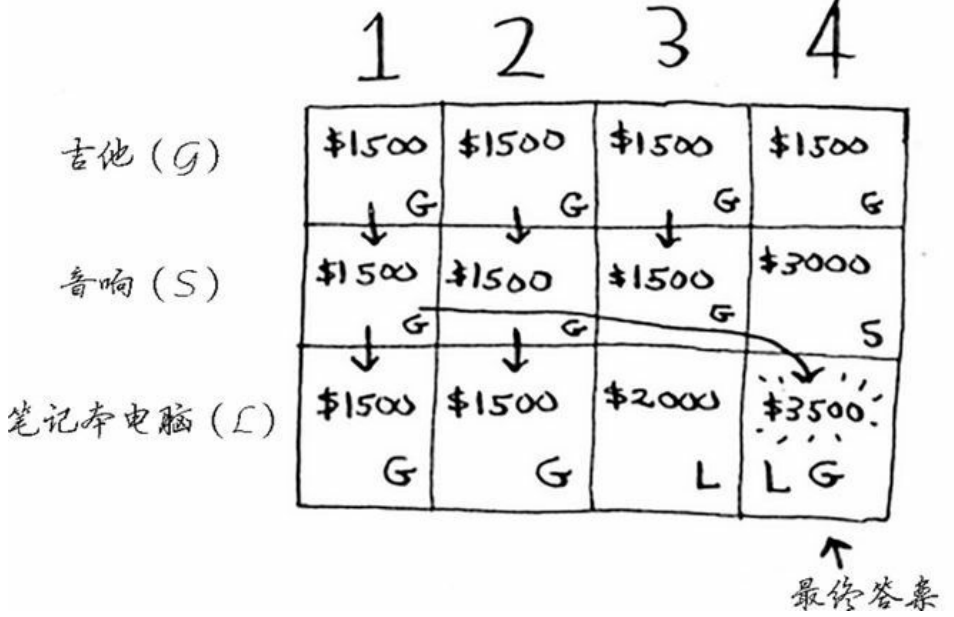
我们不难发现，其实celli=max{celli-1,price[i]+celli-1](即当前物品价值加上剩余空间最大价值)}，在计算时我们用到了前面的计算结果

例二：最大子段和

给你一个整数数组 nums ，请你找出一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。

子数组 是数组中的一个连续部分。

示例 1：

输入：nums = [-2,1,-3,4,-1,2,1,-5,4]
输出：6
解释：连续子数组 [4,-1,2,1] 的和最大，为 6 。

思路：采用动态规划法，每一个元素都有以其为结尾的数组，这个数组的最大值取值有两种情况：如果前面以num[i-1]为结尾的数组大于零，则他的值等于前面那个数组的值加上自身，如果前面那个数组小于零，则这个数组的最大值就是这个元素本身，即sum[i]=max{sum[i-1]+num[i],num[i]},当整个数组遍历完，返回sum数组里面的最大值

class Solution:
    def maxSubArray(self, nums: List[int]) -> int:
        length = len(nums)
        sum = [ i  for i  in range(length)]
        sum[0] = nums[0]
        if length > 0:
            for i in range(1,length):
                if sum[i-1] > 0:
                    sum[i] = sum[i-1] + nums[i]
                else:
                    sum[i] = nums[i]
            return max(sum)
        else:
            return nums[0]